Programme des journées Aléa 2013
Présentation des journée aléas : alea13-intro.pdf.
1) Calendrier
Le calendrier est disponible au format pdf à l'adresse: Planning des Journées Aléa 2013.
2) Cours
Les cours des journées Alea 2013 sont les suivants:
Classes de complexité probabilistes, et "calculabilité probabiliste"
Orateur : Philippe Duchon
Résumé : En algorithmique probabiliste, on définit des classes de complexité qui sont, intuitivement, proches de la classe P; je ferai un petit panorama de certaines de ces classes.
Une autre question qui sera abordée est celle de la calculabilité avec des algorithmes probabilistes.
Polycopiés : cours_duchon_1.pdf / cours_duchon_2.pdf.
Exercices : exercices_duchon.pdf.
Percolation et processus de croissance aléatoires
Orateur : Lucas Gerin
Résumé : L'objectif de ce mini-cours est de présenter les percolations de premier et de dernier passage, et leurs applications à des modèles discrets de formes croissantes aléatoires. Les outils sont assez variés : sous-additivité, percolation "classique", liens avec des systèmes de particules (TASEP), combinatoire, etc. Il n'y a pas de prérequis.
Polycopié : cours_gerin.pdf.
Énumération non récursive
Orateur : Christian Krattenthaler
Résumé : à venir.
3) Exposés longs
Les exposés longs d'Aléa 2013 sont les suivants :
Le modèle d'Ising planaire : une étude par les dimères
Orateur : Cédric Boutillier ;
Résumé : Dans cet exposé, nous présenterons quelques méthodes combinatoires pour l'étude de certains aspects du modèle d'Ising sur un graphe planaire, principalement basées sur des dimères.
On expliquera des propriétés de localité du modèle d'Ising au point critique. On étudiera aussi la géométrie des interfaces dans une configuration d'Ising XOR, obtenue comme le produit site par site de deux configurations indépendantes du modèle d'Ising.
Cet exposé sera basé en majorité sur des travaux en collaboration avec Béatrice de Tilière.
Exposé : boutillier.pdf.
Une excursion en géométrie combinatoire
Orateur : Xavier Goaoc
Résumé : Pour analyser et manipuler un objet géométrique, il est souvent pratique de lui associer une structure combinatoire qui met en lumière ses propriétés pertinentes. Cet exposé proposera un rapide tour d'horizon d'interactions entre géométrie et combinatoire à travers trois exemples classiques :
- mesure de complexité géométrique par séquences de Davenport-Schinzel,
- analyse probabiliste d'hypergraphes géométriques et
- application de théorie géométrique des graphes en géométrie des incidences.
Exposé : goaoc.pdf.
Une approche combinatoire de l'asymptotique des marches dans le quart de plan
Oratrice : Marni Mishna.
Résumé : Plusieurs approches pour trouver les formules asymptotiques pour le nombre des marches dans le quart de plan ont été récemment proposées. Cet exposé présentera une vue d'ensemble de ces progrès recents, ainsi qu'une nouvelle approche qui est simple et plutôt combinatoire. Notre méthode est assez générale, et explique un peu les différences fondamentales (et les similarités) entre les marches dans le quart de plan, et les marches dans le demi-plan.
Travail en collaboration avec Samuel Johnson (Simon Fraser) et Karen Yeats (Simon Fraser)
Exposé : mishna.pdf.
Un pont entre les espèces de structures et la combinatoire analytique.
Oratrice : Carine Pivoteau
Résumé : Le livre "Analytic Combinatorics" de Flajolet et Sedgewick propose un cadre agréable -- la Méthode Symbolique -- pour définir des classes d'objets combinatoires à partir de systèmes implicites. En se plaçant dans ce cadre, il est possible d'effectuer un certain nombre de traitements quasi-automatiques sur ces objets: manipulation de séries génératrices, génération aléatoire, analyse asymptotique, ... Cependant, lorsqu'il s'agit d'implanter de telles méthodes, il est nécessaire de se poser la question: comment savoir si un système combinatoire donné est "bien formé"? Cette question nous a amenés à considérer une autre approche permettant de décrire des objets combinatoires: la Théorie des Espèces de Structures. Bien qu'étudiées à des fins très différentes, ces deux approches présentent de nombreux points communs et permettent, lorsqu'elles sont associées, de fournir une base de travail solide pour l'automatisation d'un certain nombre de traitements combinatoires. Dans cet exposé, nous présenterons ces deux approches et nous décrirons les passerelles menant de l'une à l'autre, dans le but de caractériser les systèmes qui décrivent effectivement des structures combinatoires.
Cette présentation est basée sur un travail en commun avec B. Salvy et M. Soria.
Exposé : pivoteau.pdf.
4) Exposés courts
Inversion de Lagrange multivariée
Orateur : Axel Bacher
Résumé : Goulden et Kulkarni ont proposé une généralisation de la formule d'inversion de Lagrange à n variables. Cette formule implique une somme sur les arbres de Cayley à n+1 sommets. Ils donnent une preuve bijective de cette formule. Bousquet, Chauve, Labelle et Leroux proposent d'autres preuves bijectives. Toutes ces preuves travaillent sur des objets étiquetés, ce qui revient à multiplier la formule de Lagrange par des factorielles. Le but de cet exposé est de donner une nouvelle preuve de la formule qui s'affranchit de cette étape. Cette preuve utilise le lemme cylique, ce qui la rapproche de la preuve classique de l'inversion de Lagrange monovariée. Elle fait aussi intervenir les codes de Prüfer des arbres de Cayley.
Ce travail est en commun avec Gilles Schaeffer.
Exposé : bacher.pdf.
Non-D-finite excursions in the quarter plane
Orateur : Alin Bostan (SpecFun, INRIA Saclay)
Résumé : Counting walks in restricted lattices is a classical problem in
enumerative combinatorics and in probability theory.
In recent years, the case of walks restricted to the quarter plane 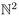 has
received special attention, and much progress has been done on the
classification of their generating series.
In this talk we report on a recent progress, obtained by blending probabilistic
and arithmetic results in an algorithmic way.
More precisely, we show that the sequence of excursions in the quarter plane
corresponding to a nonsingular nearest-neighbor walk with infinite group does
not satisfy any nontrivial linear recurrence with polynomial coefficients.
Accordingly, in those cases, the trivariate generating function of the number of
walks with given length and prescribed ending point is not D-finite.
Joint work with Kilian Raschel and Bruno Salvy.
has
received special attention, and much progress has been done on the
classification of their generating series.
In this talk we report on a recent progress, obtained by blending probabilistic
and arithmetic results in an algorithmic way.
More precisely, we show that the sequence of excursions in the quarter plane
corresponding to a nonsingular nearest-neighbor walk with infinite group does
not satisfy any nontrivial linear recurrence with polynomial coefficients.
Accordingly, in those cases, the trivariate generating function of the number of
walks with given length and prescribed ending point is not D-finite.
Joint work with Kilian Raschel and Bruno Salvy.
Exposé : bostan.pdf.
The scaling limit of the minimum spanning tree of a complete graph
Orateur : Nicolas Broutin
Résumé : We consider a complete graph 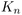 weighted with iid uniform
weights and build the minimum spanning tree
weighted with iid uniform
weights and build the minimum spanning tree 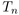 . The tree
. The tree 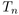 has
a attracted a lot of attention, but most informations known about its structure
are local, even the famous result of Frieze saying that the total weight of
has
a attracted a lot of attention, but most informations known about its structure
are local, even the famous result of Frieze saying that the total weight of
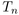 converges to
converges to 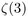 .
We are interested in the global structure of
.
We are interested in the global structure of 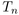 as
as 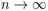 ,
and consider it as a random metric space on
,
and consider it as a random metric space on 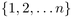 equipped with the graph distance
equipped with the graph distance 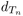 .
We show that there exists a limit compact metric space
.
We show that there exists a limit compact metric space 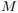 such that
such that
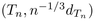 converges in distribution to
converges in distribution to 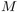 .
The metric space
.
The metric space 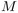 is a continuum random tree, that we prove different from
Aldous' CRT using arguments relying on its fractal dimension.
is a continuum random tree, that we prove different from
Aldous' CRT using arguments relying on its fractal dimension.
This is a joint work with L. Addario-Berry, C. Goldschmidt and G. Miermont.
Parking arborescent
Oratrice : Marie-Louise Bruner
Résumé : Les fonctions de parking ont étés introduites en 1966 par Konheim et Weiss («An occupancy discipline and applications»). Depuis, elles ont étés étudiées intensivement en raison de leur connection à l'algorithme de recherche par essai linéaire dans les tables de hachage («linear probing hashing», cf. par exemple «On the analysis of linear probing hashing», Flajolet, Poblete et Viola, 1997) et à d'autres objets combinatoires.
Nous généralisons cette notion en remplaçant les rues à sens uniques par des
arbres orientés. Plus précisément, nous introduisons
la notion de fonctions de parking pour les arbres étiquetés racinés sans
ordre sur les fils d'un nœud (labelled Cayley trees).
Dans un tel arbre à 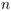 nœuds, chaque nœud est bijectivement
étiqueté par les entiers allant de 1 à
nœuds, chaque nœud est bijectivement
étiqueté par les entiers allant de 1 à 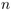 .
Comme dans la situation connue des fonctions de parking, chacune des
.
Comme dans la situation connue des fonctions de parking, chacune des
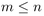 voitures a une place de parking préférée,
correspondant à un des nœuds de l'arbre et indiquée par son étiquette.
Les voitures entrent alors dans ce « système de rues ramifiées » par une
des feuilles pour arriver à leur place préférée. Si celle-ci est occupée,
elles continuent leur chemin vers la racine de l'arbre et sont garées dès qu'une
place libre apparait.
Si elle arrive à la racine sans avoir trouvé de place libre, elle quitte l'arbre et n'est pas garée.
Nous déterminons, grâce aux fonctions
génératrices liées à ce problème, le nombre exact et asymptotique des fonctions
de parking arborescentes.
voitures a une place de parking préférée,
correspondant à un des nœuds de l'arbre et indiquée par son étiquette.
Les voitures entrent alors dans ce « système de rues ramifiées » par une
des feuilles pour arriver à leur place préférée. Si celle-ci est occupée,
elles continuent leur chemin vers la racine de l'arbre et sont garées dès qu'une
place libre apparait.
Si elle arrive à la racine sans avoir trouvé de place libre, elle quitte l'arbre et n'est pas garée.
Nous déterminons, grâce aux fonctions
génératrices liées à ce problème, le nombre exact et asymptotique des fonctions
de parking arborescentes.
Une généralisation ultérieure de cette notion nous mène à étudier les
fonctions de parking sur des fonctions aléatoires de l'ensemble
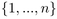 sur lui-même.
Une telle fonction
sur lui-même.
Une telle fonction 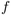 peut être représentée par un graphe orienté
à
peut être représentée par un graphe orienté
à 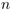 nœuds où l'arête
nœuds où l'arête 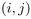 est présente ssi
est présente ssi 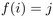 .
Les composantes connexes de ce graphe sont des cycles sur lesquels sont
greffés des arbres étiquetés.
Nous obtenons des résultats exacts et asymptotiques aussi dans ce cas-ci.
.
Les composantes connexes de ce graphe sont des cycles sur lesquels sont
greffés des arbres étiquetés.
Nous obtenons des résultats exacts et asymptotiques aussi dans ce cas-ci.
Cet exposé repose sur un travail commun avec Alois Panholzer.
Une bijection pour les cartes simples
Orateur : Gwendal Collet
Résumé : Les séries génératrices des cartes simples (sans boucles et sans arêtes multiples), et des triangulations eulériennes (ou cartes bicubiques) sont reliées par une formule très simple découverte par Marc Noy. En passant par un cas particulier de cartes simples (celles dont la face externe est triangulaire), nous présenterons une explication bijective de cette formule à l'aide d'orientations définies sur chacune des deux familles de cartes. Cette construction nous donne également un générateur aléatoire efficace (par rejet) pour les cartes simples, en fixant le nombre d'arêtes ou en fixant le nombre de sommets et d'arêtes. Travail en commun avec Olivier Bernardi et Éric Fusy.
Pyramides et diamants
Orateur : Sylvie Corteel
Travail en commun avec J. Bouttier et G. Chapuy.
Exposé : corteel.pdf.
La complexité de l'algorithme de Brzozowski est super-polynomiale génériquement.
Orateur : Sven De Felice
Résumé : L'algorithme de Brzozowski calcule l'automate minimal d'un automate quelconque en inversant celui-ci, en le déterminisant, en l'inversant à nouveau et en le déterminisant à nouveau.
Cet algorithme bien connu possède une complexité exponentielle dans le pire des cas, cependant il est réputé être plutôt efficace en pratique. Dans cet exposé, on montre qu'au contraire la complexité de l'algorithme est souvent super-polynomiale pour deux modèles de distribution des automates déterministes.
Plus précisément on montre que si on déterminise l'automate inverse d'un automate déterministe complet alors on obtient un automate avec un nombre d'états super-polynomial en le nombre d'états de l'automate de départ et ceci avec une probabilité qui tend vers 1 lorsque le nombre de sommets croît. Ce résultat s'applique lorsque la distribution des fonctions de transitions des automates déterministes complets est uniforme et lorsque chaque état est terminal avec une probabilité constante. Nous discuterons également de distributions d'automates avec très peu d'états terminaux.
Exposé : sven_de_felice.pdf.
Une généralisation de la relation de quadrangulation pour l'énumération asymptotique des hypercartes
Orateur : Wenjie Fang
Résumé : La relation de quadrangulation, découverte par Jackson et Visentin en 1990, est une relation énumérative reliant les quadrangulations ordinaires d'un certain genre et celles biparties des genres inférieurs. Malgré sa forme simple, elle a été obtenue de façon algébrique. En généralisant cette approche, nous avons obtenu une relation énumérative similaire entre les hypercartes d'un certain genre et les constellations des genres inférieurs. Avec cette relation, nous retrouvons un résultat de Chapuy sur le comportement asymptotique des hypercartes.
Exposé : fang.pdf.
Énumeration de lambda-termes d'arité bornée
Oratrice : Daniele Gardy
Résumé : Les lambda-termes, objets fondamentaux du lambda calcul, peuvent être représentés syntaxiquement par des arbres de Motzkin, auxquels on ajoute suivant certaines règles des arcs allant des noeuds unaires vers les feuilles: il s'agit alors d'une classe particulière de graphes orientés acycliques. Une vision alternative les considère comme des arbres partiellement colorés.
Nous nous intéressons ici aux termes dont tous les noeuds "unaires"
commandent le même nombre 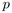 d'arcs vers les feuilles. La première
question qui se pose est d'énumérer ces termes: pour cela, nous
établissons une équation différentielle, qui nous permet ensuite
d'obtenir le comportement asymptotique de nombre de termes de taille
d'arcs vers les feuilles. La première
question qui se pose est d'énumérer ces termes: pour cela, nous
établissons une équation différentielle, qui nous permet ensuite
d'obtenir le comportement asymptotique de nombre de termes de taille 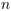 donnée. Nous nous poserons ensuite la question de savoir comment il serait
possible d'étudier plus finement ces termes, en regardant des paramètres
tels que la hauteur unaire ou la probabilité qu'un terme aléatoire soit
normalisable (au sens du lambda-calcul).
donnée. Nous nous poserons ensuite la question de savoir comment il serait
possible d'étudier plus finement ces termes, en regardant des paramètres
tels que la hauteur unaire ou la probabilité qu'un terme aléatoire soit
normalisable (au sens du lambda-calcul).
Ce travail est en commun avec O. Bodini, B. Gittenberger et A. Jacquot.
Exposé : gardy.pdf.
Characterization of limit measures of iterated cellular automata.
Orateur : Benjamin Hellouin de Menibus
Résumé : Starting from a random configuration, cellular automata exhibit a wide variety of asymptotic behaviours. These behaviours are well-described by the limit probability measure(s). In the present work, we characterized limit measures that can be reached when starting from some simple measure. Assuming the initial measure is computable, computability obstructions appear on the limit measures. Conversely, we build explicitly an automaton using auxiliary states to reach any measure satisfying those obstructions at the limit. This has decidability consequences, and this method can be extended so that the limit measures depend on the initial measure. Last, we show auxiliary states are not necessary under some additional hypotheses.
Analyse des arbres digitaux de recherche pour une source générale.
Orateurs : Brigitte Vallée et Kanal Hun
Résumé : Les arbres digitaux de recherche (dst) jouent un rôle essentiel dans les algorithmes de compression, du type Lempel-Ziv. Cette structure de données peut-être vue comme un hybride entre un arbre (binaire) de recherche (bst) et un arbre digital de type trie. L'analyse probabiliste de ses principaux paramètres (par exemple sa profondeur) s'avère donc complexe, même dans le cas où les mots sont produits par une source simple (sans mémoire ou chaine de Markov). Après les travaux fondateurs de Flajolet et Sedgewick vers 1985 (source sans mémoire), l'étude a été étendue par Jacquet, Louchard, Szpankowski et Tang à une chaine de Markov), Nous effectuons une telle analyse pour une source générale, en cherchant à étendre d'une part ces travaux fondateurs, et en les intégrant dans le point de vue général qu'a développé l'équipe dans l'étude des tries et des algorithmes de tri et de recherche.
Après avoir rappelé et comparé les trois structures de recherche (dst, bst, trie), et les principaux résultats connus sur leur analyse, nous expliquerons les principaux principes qui conduisent notre analyse. C'est un travail débuté avec Philippe Flajolet.
Exposé : vallee.pdf.
Configurations non croisées aléatoires et arbres simplement générés
Orateur : Igor Kortchemski
Résumé : On s'intéressera à différentes classes de configurations non croisées aléatoires, obtenues à partir d'un polygône en traçant des diagonales qui ne s'intersectent pas. Lorsque le nombre de sommets du polygône tend vers l'infini, ces objets discrets aléatoires convergent vers un même objet limite aléatoire. Nous verrons que l'existence de limites locales et de limites d'échelle permet d'obtenir d'intéressantes conséquences de nature combinatoire (concernant par exemple la longueur de la plus longue diagonale ou le degré maximal). Les techniques utilisées reposent sur des bijections avec des arbres de Galton-Watson (aussi connus sous le nom d'arbres simplement générés en combinatoire). Basé sur des travaux avec Nicolas Curien.
Exposé : kortchemski.pdf.
Génération aléatoire d'arbres de Motzkin “à la Rémy”
Orateur : Alice Jacquot
Résumé : Une spécification holonome est une spécification combinatoire différentielle (faisant intervenir des opérateurs de pointage) linéaire à coefficients polynomiaux. Nous donnons une telle spécification pour les arbres de Motzkin, dont nous nous servons pour obtenir un générateur de Boltzmann. Puis, nous transformons ce générateur en générateur en taille exacte, donnant en algorithme “à la Rémy”, en temps et espace linéaire en moyenne. Travail commun avec Olivier Bodini et Axel Bacher
Exposé : jacquot.pdf.
Sur le calcul du rang dans les graphes et en particulier les cliques
Orateur : Yvan Le Borgne
Résumé : En 2007, Baker et Norine ont proposé un théorème qu'ils qualifient de Riemann-Roch pour les graphes. Dans ce théorème, le rang est un paramètre entier se définissant, à l'aide d'une optimisation parmi des compositions, sur tous les étiquetages des sommets par des entiers relatifs. Une preuve de ce résultat due à Cori contient également un algorithme de calcul du rang. Nous la rappellerons dans le cadre du modèle du tas de sable et présenterons comme nouveauté une spécialisation de l'algorithme au cas des cliques. L'analyse des exécutions intéressantes de cette spécialisation gloutonne donne l'occasion de patauger dans la si rare combinatoire des nombres de Catalan, avec pour changer des bistatistiques possédant des distributions avec des symétries. C'est un travail en collaboration avec Robert Cori.
Exposé : leborgne.pdf.
Trouver les 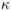 meilleurs parmi
meilleurs parmi 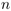 objets munis d'un rang. Un algorithme basé sur des seuils consécutifs
objets munis d'un rang. Un algorithme basé sur des seuils consécutifs
Orateur : Guy Louchard
Résumé : L'objet de cet exposé est de trouver, dans le cadre d'une suite de
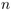 observations séquentielles d' objets, un algorithme efficace online afin
de choisir les
observations séquentielles d' objets, un algorithme efficace online afin
de choisir les 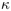 meilleurs parmi ces
meilleurs parmi ces 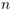 objets munis d'un rang unique.
La sélection est effectuée sans retour et l'idée est d'utiliser des
seuils qui sont fonction des sélections déja utilisées.
Notre intérêt principal réside dans le comportement asymptotique de
ces seuils lorsque
objets munis d'un rang unique.
La sélection est effectuée sans retour et l'idée est d'utiliser des
seuils qui sont fonction des sélections déja utilisées.
Notre intérêt principal réside dans le comportement asymptotique de
ces seuils lorsque 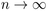 et dans la performance asymptotique de
l'algorithme-seuil correspondant.
Ceci est motivé par le fait qu'il est difficile de trouver des formes closes
pour des stratégies optimales pour des valeurs générales de
et dans la performance asymptotique de
l'algorithme-seuil correspondant.
Ceci est motivé par le fait qu'il est difficile de trouver des formes closes
pour des stratégies optimales pour des valeurs générales de
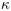 et
et 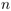 .
.
travail en coopération avec F. Thomas Bruss.
Exposé : louchard.pdf.
Équations de point fixe pour les grandes urnes de Pólya
Oratrice : Cécile Mailler
Résumé : Je m'intéresse dans cet exposé aux grandes urnes de Pólya. L'étude du comportement asymptotique d'une telle urne fait intervenir une variable aléatoire notée W. La structure arborescente de l'urne nous permet de voir W comme solution d'une équation de point fixe, et d'étudier par exemple ainsi la suite de ses moments ou l'existence d'une densité. Ce travail peut être réalisé aussi bien sur l'urne discrète elle-même que sur son plongement en temps continu. Bien que les deux variables W (associées au temps discret et au temps continu) soient différentes, elles peuvent être reliées par différentes connexions qui permettent souvent de transporter les résultats de l'une à l'autre. Ce travail est une collaboration avec Brigitte Chauvin et Nicolas Pouyanne.
Exposé : mailler.pdf.
Génération aléatoire de permutations ayant un ensemble de descentes fixé.
Orateur : M.Philippe Marchal
Résumé : L'ensemble des descentes d'une permutation 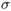 de
de 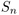 est
l'ensemble des indices
est
l'ensemble des indices ![$i\in [1,n-1]$](generated_images/idm140429410364336.png) tels que
tels que 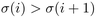 .
Nous présentons un algorithme de complexité quadratique en
.
Nous présentons un algorithme de complexité quadratique en 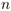 permettant d'engendrer aléatoirement et uniformément une permutation
ayant un ensemble de descentes donné. Pour certains cas, notamment pour
les permutations alternantes, une modification de l'algorithme tourne en
temps
permettant d'engendrer aléatoirement et uniformément une permutation
ayant un ensemble de descentes donné. Pour certains cas, notamment pour
les permutations alternantes, une modification de l'algorithme tourne en
temps 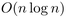 .
.
Exposé : marchal.pdf.
Marches aléatoires sur les produits libres et fonctions génératrices de chemins
Oratrice : Irène Marcovici
Résumé : Nous étudions les marches aléatoires sur les groupes (ou monoïdes) infinis de type produit libre. Le comportement asymptotique de ces marches est décrit par la mesure harmonique, qui donne la loi de la direction prise par la marche dans sa fuite vers l'infini. J. Mairesse et F. Mathéus ont montré que cette mesure a une structure markovienne. Nous prolongeons ces travaux en présentant une méthode générale pour déterminer les paramètres de la mesure harmonique. Ceux-ci sont caractérisés par des équations faisant intervenir des fonctions génératrices de chemins pondérés dans les différents groupes (ou monoïdes). Nous illustrons cette méthode par plusieurs exemples, pour lesquels elle permet également d'obtenir l'expression de la vitesse de fuite et de l'entropie. Nous retrouvons ainsi avec une démarche plus simple certains résultats déjà explorés par A. Gilch. Travail en collaboration avec Jean Mairesse.
Fin de la classification des marches à petits pas dans le quart de plan
Orateur : Steve Melczer
Résumé : L'énumération des marches à petits pas dans le quart de plan est un problème combinatoire élégant. Récemment, beaucoup de progrès ont été obtenus dans la classification des 79 marches non-équivalentes de ce type, en fonction de leurs propriétés analytiques. Nous exposerons cette classification, son utilité, et nous décrirons une méthode permettant le traitement des trois derniers cas non encore classifiés. En particulier, notre méthode définit une paramétrisation de la fonction génératrice qui éclaire la nature des ses singularités, prouvant qu'il y'en a un nombre infini. Ce travail a été réalisé conjointement avec Marni Mishna.
Exposé : melczer.pdf.
Hauteur de l'arbre de Lyndon
Orateur : Lucas Mercier
Résumé : Tout mot de Lyndon de longueur au moins 2 peut être décomposé de manière canonique en deux mots de Lyndon. En itérant cette décomposition, on associe à tout mot de Lyndon un arbre binaire, appelé arbre de Lyndon. Le but de cet exposé est de présenter quelques idées qui ont permis de calculer la hauteur asymptotique de l'arbre de lyndon associé à un mot choisi uniformément parmi les mots de Lyndon de longueur n.
Exposé : mercier.pdf.
Variance d'une marche aleatoire avec contrainte
Orateur : Philippe Nadeau
Notes : nadeau.pdf.
Temps d'attente dans l'évolution d'ADN et analyse par "clumps"
Orateur : Pierre Nicodeme
Résumé : Nous partons d'un modèle d'évolution infinitésimal défini sur les lettres de l'ADN, et d'une distribution initiale sur les lettres. Nous considèrons alors une séquence aléatoire d'ADN ne contenant pas un k-mer ou mot de longueur k et calculons la probabilité qu'après une unité de temps, sous le modèle d'évolution, le k-mer apparaisse au moins une fois dans la séquence. Une analyse par clumps, soit par automates, soit par combinatoire des mots, montre que cette probabilité a un comportement quasi-linéaire en fonction de la longueur de la séquence, quand cette longueur n'est pas trop grande; le temps d'attente d'apparition d'un k-mer est l'inverse de la probabilité considérée, et il se comporte donc comme une fonction hyperbolique de la longueur.
Ce travail fait suite à des travaux précédants avec Sarah Behrens et Cyril Nicaud.
Exposé : nicomede.pdf.
On the probability of planarity of a random graph near the critical point
Orateur : Juanjo Rué (ICMAT-Madrid)
Résumé : Let 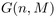 be the uniform random graph with
be the uniform random graph with 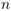 vertices and
vertices and 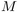 edges.
Erdős–Rényi (1960) conjectured that the limiting probability
edges.
Erdős–Rényi (1960) conjectured that the limiting probability
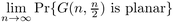
exists and is a constant strictly between 0 and1 1. Łuczak, Pittel and Wierman (1994) proved this conjecture and Janson, Łuczak, Knuth and Pittel (1993) gave lower and upper bounds for this probability.
Our contribution is the computation of the exact limiting probability of a
random graph being planar near the critical point 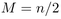 : for each
: for each
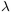 , we find an exact analytic expression for
, we find an exact analytic expression for
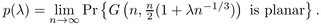
In particular, we obtain 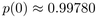 . We also extend these
results to classes of graphs closed under taking minors. If time permits,
further extensions will be discussed.
. We also extend these
results to classes of graphs closed under taking minors. If time permits,
further extensions will be discussed.
This is a joint work with Marc Noy (UPC) and Vlady Ravelomanan (LIAFA).
Exposé : rue.pdf.
Une extension stochastique du modèle du tas de sable sur un graphe
Orateur : Thomas Selig
Résumé : Dans le modèle du tas de sable, lorsqu'un sommet devient instable, c'est-à-dire que le nombre de grains en ce sommet dépasse son degré, celui-ci s'éboule en envoyant un grain vers chacun de ses voisins. Dans notre modèle, un sommet instable envoie un grain vers chaque voisin avec probabilité p>0 (indépendamment pour chaque voisin). On donnera une caractérisation des états récurrents de ce nouveau modèle, en termes d'orientations du graphe. De plus, on introduira un olynôme comptant ces états récurrents selon leur nombre (total) de grains de sable, et on verra que celui-ci satisfait une relation de récurrence qui ressemble celle du polynôme de Tutte.
Exposé : selig.pdf.
Prolongement analytique de la mesure spherique -- Analytic continuation of spherical measures
Orateur : Andrea Sportiello
Abstract : Consider 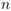
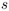 -dimensional real vectors
-dimensional real vectors 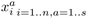 ,
and call
,
and call 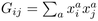 the scalar product. The integral of a
function
the scalar product. The integral of a
function 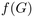 depending on scalar products only (i.e., "spherically
invariant") has a simple behaviour in s, that allows for an analytic
continuation, of s from
depending on scalar products only (i.e., "spherically
invariant") has a simple behaviour in s, that allows for an analytic
continuation, of s from 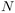 to
to 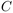 . The reason is that the change of
variables from
. The reason is that the change of
variables from 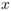 to
to 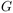 has a simple Jacobian (a power of
has a simple Jacobian (a power of 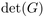 ). The
rigorous analytic continuation requires a comprehension of the
distribution
). The
rigorous analytic continuation requires a comprehension of the
distribution 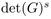 that, following the seminal idea of Bernstein,
passes through the Cayley Identity,
that, following the seminal idea of Bernstein,
passes through the Cayley Identity, 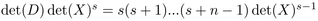 .
All of this is known.
.
All of this is known.
Our original contribution is to generalise the approach to the case of
vectors on the unit sphere, i.e. to the extra constraints 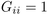 .
This requires a new Cayley Identity (for which we provide a combinatorial
proof using Grassmann-Berezin calculus), and involves Spanning Forests.
.
This requires a new Cayley Identity (for which we provide a combinatorial
proof using Grassmann-Berezin calculus), and involves Spanning Forests.
A general framework for the realistic analysis of sorting and searching algorithms. Application for some popular algorithms.
Oratrice : Thu Hien Nguyen Thi
Résumé : As there are some algorithms which deal with keys (viewed as a whole
structure) and some others which deal with symbols, it is not easy to
compare their efficiency. Furthermore, since in most real-life
situations a key is complex and cannot be reduced to a single machine
word, it is not realistic to consider the comparison between two keys
as a unitary comparison. That is why Sedgewick proposed in 1998 to
unify the analyses of basic sorting and searching algorithms by
studying on the average the number of symbol comparisons between keys
(seen as words). First results are due to Fill and Janson, Fill and
Nakama who analyzed QuickSort and QuickSelect, but only
on data composed of random uniform bits. Then, Clément, Fill,
Flajolet and Vallée extend the previous analyses when data are words
emitted by a general source. In the present work, we draw a general
framework for such realistic analyses: we provide an "automatic"
method which takes as an input the probability of comparing two random
words for a given algorithm and computes the exact formula for the
average number of symbol comparisons. This method is applied to three
popular algorithms: Insertion Sort, Bubble Sort and
Minimum Selection. We also recover the results of
QuickSort and QuickSelect. The results are the
following: with respect to key comparisons, the average-case
complexity of QuickSort is asymptotic to 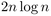 ,
Insertion Sort to
,
Insertion Sort to 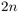 , BubbleSort to
, BubbleSort to 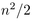 ,
QuickMin to
,
QuickMin to 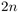 , Selection Min to
, Selection Min to 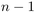 . With respect
to the number of symbol comparisons, the complexity becomes of
respective order
. With respect
to the number of symbol comparisons, the complexity becomes of
respective order 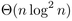 ,
, 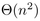 ,
, 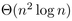 for sorting algorithms and remains
for sorting algorithms and remains 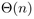 for Selection
algorithms. We further discuss the change in the complexity measure of
the algorithms, from the number of key comparisons to the number of
symbol comparisons and also the different constants arising in the
analysis reflecting the mixing between algorithms and the way data are
produced.
for Selection
algorithms. We further discuss the change in the complexity measure of
the algorithms, from the number of key comparisons to the number of
symbol comparisons and also the different constants arising in the
analysis reflecting the mixing between algorithms and the way data are
produced.
joint work with Julien Clément and Brigitte Vallée
Exposé : nguyen_thi.pdf.
Cutting Down Birthday Trees and Inhomogeneous Continuum Random Trees
Orateur : Minmin Wang
Résumé : The birthday tree is a model of random labeled trees introduced by Aldous, Camarri and Pitman as a generalization of Cayley tree (uniform labeled tree). In this model, weights are used to introduce inhomogeneity among the vertices. We consider the following fragmentation process on a birthday tree: choose a random vertex according to the weights and, by removing it, split the tree into several components; repeat this procedure for each component until all the vertices have been picked. There is a natural "cut-tree" that describes the genealogy of the fragmentation process. We show that there is a simple backward transformation which recovers the initial tree from the cut-tree, so that a tree and its cut-tree appear as dual with respect to the transformations. We use these observations for finite trees and weak convergence arguments to prove corresponding results for inhomogeneous continuum random trees (ICRT), which are random metric space that are scaling limits of birthday trees. The limit picture for the ICRT imply a number of recent results on the number of cuts required to isolate finitely many vertices from random trees. This is a joint work with Nicolas Broutin.
Propriétés asymptotiques de certaines familles de graphes à mineurs exclus
Oratrice : Kerstin Weller
Résumé : On s'intéresse au comportement asymptotique de classes de graphes étiquetés fermées par extraction de mineurs. Ces classes sont décrites par une liste de mineurs interdits. Grâce aux travaux de McDiarmid et de ses collaborateurs, le comportement d'un graphe typique d'une telle classe est bien compris quand les mineurs interdits sont 2-connexes. C'est par exemple le cas des graphes planaires ou des forêts. Dans cet exposé, nous étudions des classes dont certains des mineurs interdits ne sont pas 2-connexes, et montrons que leurs propriétés asymptotiques peuvent être très différentes de celles obtenues dans le cas de mineurs 2-connexes. Nous classons nos exemples selon la nature de la (des) singularité(s) dominante(s) de la série qui compte les graphes connexes, car elle semble régir les propriétés asymptotiques. Ces résultats constituent un premier pas vers une classification complète des classes de graphes fermées par extraction de mineurs.
(travail en commun avec Mireille Bousquet-Mélou, Bordeaux)
Exposé : weller.pdf.
